Can you solve it? Pi Day puzzles that will leave you pie-eyed
Two teasers – one gyral and one viral – to usher in the annual celebration of maths

Hi guzzlers.
Tomorrow is Pi Day – March 14 – the annual excuse for the mathematical community to circulate puns about buns. I mean to honour pi, the ratio of a circle's circumference to its diameter, which to two decimal places is 3.14, hence 3/14, as the Americans write tomorrow's date.
In recent years Pi Day has gone from a geeky American eccentricity to a global celebration of maths, and I'm getting my r's in a day early with two puzzles from the brilliant minds at Brilliant.org. (That's r for radius, obvs.)
The first is all about pie, in all its homonymic glory. Pictured below are three identical boxes packed with pies. Which box contains the most pie?

You can assume that all pies are exactly the same height.
The next question is about a virus. One hundred computers are connected in a 10x10 network grid, as below. At the start exactly nine of them are infected with a virus. The virus spreads like this: if any computer is directly connected to at least 2 infected neighbours, it will also become infected.
Will the virus infect all 100 computers?
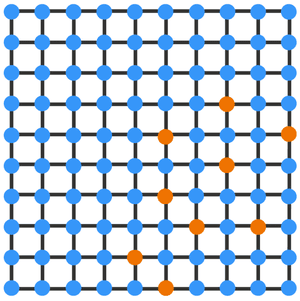
The image shows a possible example of the initial infection. You can try to fill it in to see if ultimately the network will consist of 100 orange dots. But the question is not asking what happens to this example. I want to know what will happen given any initial configuration of infected computers.
It's a lovely question - or rather, the solution is lovely. (And there is a connection to pi, but not an obvious one). Have a think, and then submit your answers to both questions here.
This week's puzzles come from a corner of the web where Pi Day is highly celebrated! Brilliant.org is a website of maths and physics problems that has more than 4 million registered members. It's a bit like the world's very own after-school maths and science club.
Sue Khim, CEO of Brilliant.org, says: "Brilliant is a community of people who love a challenge in math, science, and engineering. We bring together students, educators, professionals, olympiad champions, and enthusiasts from around the world. Our community pushes and supports each other as they stretch themselves as problem solvers. Our members contribute problems and articles – people introduce each other to their favorite topics and ideas. And each week, we curate the best 15 problems in our Problems of the Week. We also publish Explorations: popular guided problem-solving courses, which are built on our principles for learning. We welcome thinkers and problem solvers of all types and ages to join our community!"
Brilliant keeps the data on all its multiple choice questions - and has kindly provided me with their figures for today's two puzzles. So when I post the solutions, we'll be able to see how the readers of this column compare to the global community of brillianters. Shine on, you crazy diamonds!
In the comments below, please NO SPOILERS! Please discuss pies, Pi Day and the virality of puzzles.
I'll be back at 5pm GMT with the solutions, explanations and poll results.
UPDATE: The answers and results are now live here.
I set a puzzle here every two weeks on a Monday. Send me your email if you want me to alert you each time I post a new one.
I'm always on the look-out for great puzzles. If you would like to suggest one, email me.
My puzzle book Can You Solve My Problems: Ingenious, Perplexing and Totally Satisfying Math and Logic Puzzles is just out in the US. It is already out in the UK with a slightly different subtitle. I'm also the co-author of the children's book Football School: Where Football Explains The World, which was a runner-up in the Blue Peter Book Awards 2017.
Since you're here …
… we have a small favour to ask. More people than ever are regularly reading the Guardian, but far fewer are paying for it. Advertising revenues across the media are falling fast. And unlike many news organisations, we haven't put up a paywall – we want to keep our journalism as open as we can. The Guardian's independent, investigative journalism takes a lot of time, money and hard work to produce. But we do it because we believe our perspective matters – because it might well be your perspective, too.
If you regularly read and value our reporting, support us now and help make our future much more secure.



















