sec1 area, volume (fr Keith)

sec1 area, circles (fr Keith)

sec1 geometry n algebra (fr Keith)

sec1 pattern (fr Keith)

P6 area and perimeter (fr YZ)

P6 speed (fr YZ)

P6 speed (fr YZ)

P6 Speed (fr YZ)

P6 speed (fr YZ )

P5 math (fr Richie)

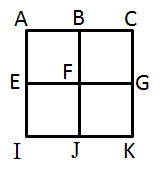
Counting (number of pairs of perpendicular and parallel lines) ( combinatorics)

For each of the figures below, find the number of:
(a) parallel lines (including line segments) 

(b) perpendicular lines (including line segments) 

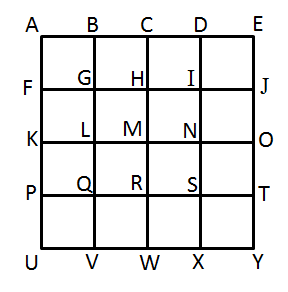
> For each of the figures below, find the number of
> (a) parallel lines (including line segments)
> (b) perpendicular lines (including line segments)
>>

P5 whole numbers, internal transfer (fr tianle)

P5 Ratio, external transfer (Fr: CCL)

Q1.

The ratio of the number of boys to the number of girls in a school is 7 : 6. 

After twice as many boys as girls left the school, the ratio became 4 : 5 .  

There were 575 girls in the school in the end.

(a)  How many girls were in the school at first?

(b)  How many more boys than girls left the school?

Q2. 

The ratio of the number of boys to the number of girls in a school is 7 : 6. 

After some girls joined the school and twice as many boys left the school, the ratio became 4 : 7 .

There were 931 girls in the school in the end.

(a)  How many girls were in the school at first?

(b)  How many boys left the school?

____

The above were modified question from...

P3 whole numbers, counting (fr ccl )

P5 fraction, percentage (fr PW)

P5 Whole numbers, money (fr TL)

P5 percentage (fr YZ )

P5 Area of triangles (fr PW)

P5 fraction (fr yong yew)

P5 rate (fr ranice tang)

There were 3 taps. They were installed to fill up a tank with water. When Tap A and B were turned on at the same time,they took 3 hours to fill up half of the tank. When Tap B and C were turned on at the same time,they took 12 hours to fill up the tank completely. When Tap A and C were turned on at the same time,they took 4 hours to fill up the tank conpletely. How long would it take for the 3 taps to fill up the tank completely with water if they were all turned on at the same time?


Sent from my iPhone

P5 area of triangle (fr Clara)

Note:

For a P5 pupil who is solving this problem, so sorry, but you are forced to ASSUME that the shaded triangle at the bottom is an equilateral triangle, else it can't be solved.  With that ASSUMPTION, one can then arrive at the final answer that the entire shaded area is 88cm2.

But this is so sad, as we should NEVER have to make such dangerous assumptions.  Pupils who are very careful will be very hesitant to make this assumption and hence will waste precious time trying to solve this problem.

For a secondary school pupil, no assumption is needed as you can prove, by application of Pythagoras Theorem and then via algebraic manipulation, that the base of the isosceles triangle at the bottom is approx 4.04cm, which is about 4, or a third of 12 .  With this finding, it goes to prove that the assumption is needed for the poor P5 kid, which again I am so sorry for those P5 pupils who had to sit for this question under a real exam setting!  ><

** Look out for another question that I will be crafting to prove that the paper can be similarly folded yet not achieving a near equilateral triangle at the bottom! ><

P5 fraction and percentage (fr grace)

P5 math (fr grace)

P5/P6 Area (fr NMOS)

P5/P6 numbers, counting (fr NMOS)

P5/P6 Geometry (Fr NMOS)

P5/P6 geometry (fr NMOS)

P5/P6 geometry (fr NMOS)

P5/P6 geometry (fr NMOS)

(Hint: construct an equilateral triangle using one of the lines )

P5/P6 geometry (fr NMOS)

P5/P6 geometry (fr NMOS)

P5/P6 geometry (fr NMOS)

Sec 1 Geometry (Fr: CKM)

P5 fraction and ratio (fr CCL, modified from heuristics worksheet)

P5 fraction (fr CCH)

Sec1 algebra (fr Priscilla )

P6 fractions (fr Aitong ppr, via Sheryl t)

P6 percentage (fr Aitong pri. Via Sheryl t)

P6 numbers, counting "frog and pond" (fr Aitong pri. Via Sheryl t)

P5 Percentage ( fr Richie )

> A fruit seller had 10% more oranges than apples. After selling 20 apples and 48 oranges, he had 90% as many oranges as apples. Find the number of oranges he had in the end.

P5 Average (an extension question by CCL)

James wrote a few numbers on a piece of paper and calculated the average of the value of these numbers.

If James wrote another, 10, on the paper, the average would be reduced by 1.

If he wrote the number 106 instead, the average would be increased by 3.

(a) How many numbers did he write on the piece of paper originally?

(b) What was the original average value?

Modified from 

http://cclmath.blogspot.sg/2013/09/p5-average-fr-max-taken-fr-nanyang-pr.html

P5 numbers (fr koobits, NMOS via Sylvia c)

1/9/15 5:23:18 pm: Sylvia Chang (5c15):

300 people stand in a row.
Starting from the first person on the LEFT, each person calls out a number in this pattern: 1,2,3,1,2,3,1,2,3...
Starting from the first person on the RIGHT, each person calls out a number in this pattern:1,2,3,4,1,2,3,4,1,2,3,4...
How many people call out the number 2 twice?


Sent from my iPhone

P5 Olympiad, number pattern (fr YZ)

For a box, similarly drawn, that has a sum of 888, what are all the numbers in that box?

P5 fractions (fr foo ck )